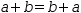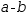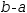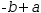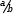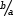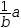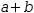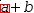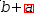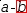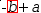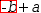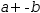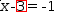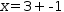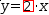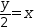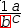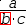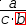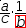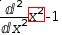3.2.1 Commute

The left- and right- move actions transform expressions by rearranging the order of operands. Mathematically, binary operators like addition and multiplication are commutative, meaning that changing the order of operands does not change the result. That is, 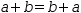a+b=b+a. Using the move tools, either operand of addition or multiplication can be selected and moved to the other side of the operator.

In contrast, subtraction and division are not commutative. This means that moving b lef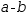t in a-b cannot result in 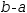b-a because that would change the mathematical meaning of the expression. But mathematical correctness is preserved by introducing a negation to produce 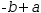-b+a. Similarly, moving b lef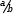t in a/b cannot result in 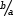b/a. Here, mathematical correctness is preserved by introducing an inversion to produce 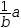1÷b⋅a.

To see how the move actions work, enter the expression 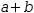a+b, select a and touch → . The expression changes from 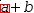.{a}+b to 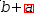b+.{a}. After the change, touching ← reproduces the original expression.

Now try ← with 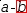a-.{b}. Note that the expression becomes 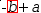-.{b}+a. Touching → transforms back to the original. However, expanding the selection of b to include the negation and then touching → produces a slightly different result. 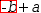.{-b}+a moved right becomes 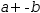a+-b.

The effect of ← and → can also be achieved by swiping left or right. But be careful: a swipe starts with a down touch which may cause the selection to be extended. Wait for the selection box to revert from red to black before beginning the swipe.

The move tools make use of commutativity where possible and preserve mathematical correctness in other cases. For example, when an additive operand is moved across a relational operator, it changes sign. Try it with 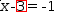x-.{3}=-1. Touching → moves 3 to the other side of the equation to yield 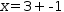x=3+-1. Similarly, applying ← to 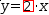y=.{2}⋅x yields 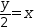y÷2=x.

Moving b right in 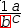1÷.{b}⋅(a÷c) yields 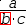a÷(.{b}⋅c). Moving it right twice more yields 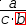a÷(c⋅.{b}) and 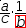a÷c⋅(1÷.{b}). Moving b left three times recovers the original expression.

Operands can also be moved out of complex constructs like summations, derivatives and integrals within the rules of algebra. For example, ← applied to 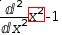ⅆ.{x^2}-1ⅆx:2 yields ⅆx^2ⅆx:2-ⅆ1ⅆx:2. Refer to the documentation for each construct to see how left and right moves are interpreted by the construct.